|
 Базисным понятием всей теории информации является понятие
энтропии. Базисным понятием всей теории информации является понятие
энтропии.
Энтропия – мера неопределенности некоторой ситуации.
Если мы вводим меру неопределенности f , то
естественно потребовать, чтобы она была такова, чтобы
во-первых, неопределенность росла с ростом числа возможных
исходов, а во-вторых, неопределенность составного опыта была
равна просто сумме неопределенности отдельных опытов, иначе
говоря, мера неопределенности была аддитивной: f(nm)=f(n)+f(m).
Именно такая удобная мера неопределенности была введена К.
Шенноном:
H(X)= —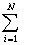 P
(Xi) log P (Xi), P
(Xi) log P (Xi),
где Х –
дискретная случайная величина с диапазоном изменчивости N,
P(Xi) – вероятность i – го уровня X.
В теории
информации в формуле для энтропии обычно используют двоичные
логарифмы, тогда (энтропия и информация) измеряется в битах.
Это удобно тем, что выбор между двумя равновероятными
уровнями Xi (как в двоичном) сигнале
характеризуется неопределенностью 1 бит.
Иногда пользуются десятичными
логарифмами и единицей энтропии является дит.
 В физике удобнее пользоваться натуральными логарифмами и
единицей энтропии является нат В физике удобнее пользоваться натуральными логарифмами и
единицей энтропии является нат
Выбор основания – лишь вопрос масштаба, в любом случае
энтропия безразмерна. Возможная величина энтропии заключена
в пределах:
0£ H(X)£ logN.
Нижняя грань соответствует вырожденному распределению.
Неопределенность величинs Х отсутствует. Верхняя грань
соответствует равномерному распределению. Все N значений Xi
встречаются с равной вероятностью.
Если
две случайные величины X и Y, каким-то образом связанные
друг с другом (например на входе и выходе какой-то системы)
, то знание одной из них, очевидно уменьшает
неопределенность значений другой. Остающаяся
неопределенность оценивается условной энтропией. Так,
условная энтропия Х при условии знания Y определяется как:
H(X|Y)=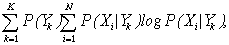
г де
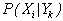 – условные
вероятности (вероятность i-го
значения X при условии Y=Yk), диапазоны
изменчивости X и Y (соответственно N и K) не обязательно
совпадают. – условные
вероятности (вероятность i-го
значения X при условии Y=Yk), диапазоны
изменчивости X и Y (соответственно N и K) не обязательно
совпадают.
Чтобы
рассчитать H(X|Y), рассчитывают К энтропий Х,
соответствующих фиксированному Yk и затем
суммируют результаты с весами P(Yk). Очевидно,
условная энтропия меньше безусловной, точнее:
0£ H(X|Y)£ H(X).
Нижняя
грань соответствует однозначной зависимости Х от Y, верхняя
– полной независимости.
Информация определяется разностью между безусловной и
условной энтропиями. Это уменьшение неопределенности “знания
чего-то за счет того, что известно что-то”. При этом
замечательно, что информация I симметрична, т.е. IYX=IXY:
IXY=H(X)-H(X|Y)=H(Y)-H(Y|X)= IYX.
 Информация всегда неотрицательна; она равна нулю, когда Х и
Y независимы; информация максимальна и равна безусловной
энтропии, когда между Х и Y имеется однозначная зависимость.
Таким образом, безусловная энтропия – это максимальная
информация, потенциально содержащаяся в системе (вариационном
ряде). Заметим, что мы сказали однозначная, но не
взаимно-однозначная зависимость. Это значит, что несмотря на
симметрию, верхние грани IXY и IYX
отличаются: Информация всегда неотрицательна; она равна нулю, когда Х и
Y независимы; информация максимальна и равна безусловной
энтропии, когда между Х и Y имеется однозначная зависимость.
Таким образом, безусловная энтропия – это максимальная
информация, потенциально содержащаяся в системе (вариационном
ряде). Заметим, что мы сказали однозначная, но не
взаимно-однозначная зависимость. Это значит, что несмотря на
симметрию, верхние грани IXY и IYX
отличаются:
0£ I XY£
H(X), 0£ IYX£
H(Y).
Как это может быть? Положим, XÞ Y (но
обратное неверно). Тогда H(Y|X)=0, H(X|Y)¹ 0, IYX=H(Y)=
IXY. Очевидно, это возможно только когда H(X)>H(Y).
Информация – это всего лишь характеристика степени
зависимости некоторых переменных.
|