Задание 1.

1. Дан n-мерный вектор х=(х1, х2, ...,хn). Написать программу, которая переставляет компоненты вектора х так, чтобы в начале стояли положительные, затем нулевые и отрицательные значения в порядке их следования.

2. Даны векторы а=(a1, a2, a3) и b=(b1, b2, b3). Написать программу вычисления скалярного и векторного произведений этих векторов

3. Даны m векторов x1=(x11, x21, x31), ..., xm=(x1m, x2m, x3m). Написать программу нахождения суммы этих векторов.

4. Даны три вектора а=(a1, a2, a3), b=(b1, b2, b3), с=(с1, с2, с3). Написать программу вычисления смешанного произведения этих векторов.

5. Даны два вектора а=(a1, a2, a3), b=(b1, b2, b3). Написать программу, которая находит угол между этими векторами.

6. Даны векторы а=(a1, a2, a3), b=(b1, b2, b3), с=(с1, с2, с3), d=(d1, d2, d3). Написать программу, вычисляющую скалярное произведение (ахb)*(cxd).

7. Даны две точки в n-мерном пространстве X=(х1, х2, ..., хn), Y=(y1, y2, ...,yn). Написать программу нахождения расстояния между этими точками и вектора XY.

8. Дан n-мерный вектор х=(х1, х2, ...,хn). Написать программу, которая может находить вектор y=(xn, xn-1, xn-2, ..., x2, x1) и скалярное произведение x*y.

9. Дан вектор а=(a1, a2, a3) и плоскость, заданная уравнением Ах+Ву+Сz=0. Написать программу нахождения угла между векторами и плоскостью.

10. Даны векторы в n-мерном пространстве х=(х1, х2, ...,хn), у=(у1, у2, ...,уn), z=(z1, z2, ...,zn). Написать программу, которая определяет, можно ли из этих векторов построить треугольник и, если можно, найти его площадь.

11. Даны два вектора х=(х1, х2, ..., хn), у=(у1, у2, ..., уn). Написать программу, проверяющую является ли х и у линейно зависимыми.

12. Даны три вектора а=(a1, a2, a3), b=(b1, b2, b3), с=(с1, с2, с3). Написать программу нахождения вектора F=(a*b)*c.

13. Дан вектор х=(х1, х2, ...,хn). Написать программу, которая находит разность между первой и последней отрицательными координатами вектора х.

14. Дан вектор х=(х1, х2, ...,хn). Написать программу, которая проверяет, упорядочены ли его координаты по убыванию.

15. Даны три вектора, образующие треугольник а=(a1, a2, a3), b=(b1, b2, b3), с=(с1, с2, с3). Написать программу, вычисляющую площадь проекции этого треугольника на плоскость Ax+By+Cz+D=0.

Задание 2.

1. Дана матрица А(nxn) и вектор а = (a1, a2, ..., an). Написать программу вычисления вектора b = A*a.

2. Дана матрица А(nxn). Построить n-мерный вектор по правилу: если в строке матрицы с номером i есть отрицательные элементы, то bi = 0, в противном случае bi = 1.

3. Даны две матрицы А(nxn) и B(nxn). Написать программу нахождения произведения этих матриц D = A*B.

4. Дана матрица А(nxn). Написать программу, которая меняет к-ю и m-ю строки матрицы, а затем транспонирует матрицу.

5. Дана матрица А(nxn) и вектор х = (х1, х2, ...,хn). Написать программу нахождения скалярного произведения (х*Ах).

6. Дана матрица А(nxn). Написать программу нахождения матрицы Ат*А, где Ат - транспонированная матрица.

7. Даны две матрицы А(nxn) и B(nxn). Написать программу нахождения матрицы, равной (А-В)т.

8. Даны два вектора b = (b1, b2, ..., bn), x = (x1,x2, ..., xn) и матрица А(nxn). Написать программу вычисления длины вектора Ах - b.

9. Дана матрица А(nxn). Написать программу, которая вычеркивает столбец с номером р и переставляет остальные так, чтобы получилась матрица nx(m-1).

10. Даны две матрицы А(nxn) и B(nxn), а также два вектора х = (x1, x2,..., xn) и y = (y1, y2, ..., yn). Написать программу нахождения скалярного произведения (Ах)*(Ву).

11. Даны две матрицы А(nxn) и C(nxn). Написать программу вычисления матрицы Ст*(А+С), где Ст - транспонируемая матрица.

12. Дана матрица А(nxn). Написать программу, которая находит максимальный по абсолютной величине элемент и переставляет строки и столбцы так, чтобы он оказался в левом верхнем углу.

13. Даны две матрицы А(nxn) и B(nxn). Написать программу нахождения суммы диагональных элементов А*В.

14. Дана матрица А(nxn). Написать программу поиска одинаковых элементов в этой матрице.

15. Дана матрица А(nxn). Написать программу нахождения максимального элемента матрицы, принадлежащего отрезку [p, q].

Задание 3.

1. Дана матрица А(nxn). Написать программу нахождения минимального элемента из (max1, ...,maxn), где maxi - максимальный в i - той строке.

2. Даны две матрицы А(nxn) и B(nxn). Написать программу получения коммутатора АВ этих матриц.

3. Дана матрица А(nxn). Написать программу, которая упорядочивает строки этой матрицы по убыванию первых элементов строк.

4. В матрице А(nxn) найти максимальный и минимальный элементы. Указать их разность, а также строки и столбцы, на пересечении которых они находятся.

5. Даны квадратные матрицы А(nxn), B(nxn), C(nxn). Написать программу вычисления матрицы (А+В)*С.

6. Дана матрица А(nxn). Написать программу вычисления матрицы АК, где К>0 - целое число.

7. Дана матрица А(nxn). Написать программу, которая упорядочивает элементы этой матрицы по возрастанию.

8. Дана матрица А(nxn). Написать программу, которая находит максимальный и минимальный элементы этой матрицы и переставляет столбцы и строки так, чтобы эти элементы поменялись местами.

9. Дана матрица А(nxn). Написать программу вычисления max(Sk), где .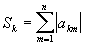

10. Дана матрица А(nxn). Написать программу, которая находит максимальную сумму элементов, стоящих на диагоналях, параллельных данной.

11. Даны две матрицы А(nxn) и B(nxn). Написать программу нахождения максимального значения max(S1, S2, ..., Sn), где Sk - скалярное произведение к - й строки матрицы А на к - й столбец матрицы В.

12. Даны m векторов х1 = (х11, х21, ...,хn1), ..., xm = (x1m, x2m, ...,xnm). Написать программу поиска вектора минимального по длине.

13. Даны две матрицы А(nxn) и B(nxn). Написать программу вычисления матрицы 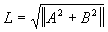, где норма ||C|| матрицы С есть max||Ckm|| .

14. Дана матрица А(nxn) с положительными элементами. Написать программу, которая находит среди элементов матрицы тройки таких элементов (aji-1, aji, aji+1), чтобы существовал треугольник со сторонами, равными этим числам.

15. Даны три вектора a = (a1, a2, ...,an), b = (b1, b2, ..., bn), c = (c1, c2, ...,cn). Написать программу, которая проверяет зависимость этих векторов.

Задание 4.

1. Дана прямоугольная матрица А(nxn). Заменить наименьший элемент каждой строки, начиная со второй, наибольшим элементом предыдущей строки.
2. Дана действительная квадратная матрица порядка n. Построить последовательность действительных чисел A1, A2, ..., An по правилу: если в i - той строке матрицы элемент, принадлежащий главной диагонали, отрицателен, то Ai равно сумме элементов i - той строки, предшествующих первому отрицательному элементу; в противном случае Ai равно сумме последних элементов i - той строки, начиная с первого по порядку неотрицательного элемента.
3. Дана действительная квадратная матрица порядка n. Вычислить сумму тех ее элементов, расположенных на главной диагонали и выше нее, которые превосходят по величине все элементы, расположенные ниже главной диагонали. Если на главной диагонали и выше нее нет элементов с указанным свойством, то ответом должно служить сообщение об этом.
4. Заданы квадратная матрица А порядка n и число К(1<=К<=n). Столбец с минимальным по модулю элементом в К - той строке переставить с К - тым столбцом.
5. Задана квадратная матрица порядка n. Исключить из нее строку и столбец, на пересечении которых расположен минимальный элемент главной диагонали.
6. Дана матрица А(nxn). Найти максимальный по модулю элемент матрицы. Переставить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент матрицы был расположен на пересечении К - той строки и К - того столбца.
7. Дана целочисленная матрица размерностью nxm. Найти матрицу, получающуюся из данной перестановкой строк - первой с последней, второй с предпоследней и т.д.
8. Дана целочисленная матрица размерностью nxm, целые числа к, l (1<=k<=n, 1<=l<=n, k<>l). Преобразовать матрицу так, чтобы строка с исходным номером к непосредственно следовала за строкой с исходным номером l.
9. Найти все различающиеся элементы целочисленной квадратной матрицы размерностью nxm.
10. Дана матрица А(nxn). Написать программу, которая упорядочивает строки этой матрицы по убыванию первых элементов ее строк.
11. Дана матрица А(nxn). Написать программу, которая упорядочивает строки этой матрицы по возрастанию.
12. Дана матрица А(nxn). Написать программу, которая находит максимальную из сумм элементов, стоящих на диагоналях, параллельных главной диагонали.

назад содержание вперед