Пусть Aц- целое десятичное число. Тогда в его разложении отсутствуют коэффициенты с отрицательными индексами, и его можно представить в виде:
Aц=an-1*2n-1+an-2*2n-2+...+a0*20
Разделим число Aц на 2. Частное будет равно
an-1*2n-2+...+a1
а остаток равен a0
Полученное неполное частное опять разделим на 2, остаток от деления будет равен a1
Если продолжить процесс деления, то на n-м шаге получим набор цифр
a0, a1, a2..., an-1
которые входят в двоичное представление числа Aц и совпадают с остатками при последовательном делении данного числа на 2. Но мы их получили в порядке, обратном порядку расположения числа Aц:
Aц=an-1an-2...a1a0
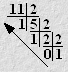
Пример: Перевести десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) удобнее изобразить так:

Записывая остатки от деления в направлении, указанном стрелкой, получим:1110=10112
1)Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2)последовательно умножать данное число и получаемые дробные части произведений на основе новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3)полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4)составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример: Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.

Здесь вертикальная черта отделяет
целые части чисел от дробных частей.
Отсюда: 0.187510=0.00112=0.148=0.316
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно.
При переводе в восьмеричную систему счисления двоичное число разбиваем на группы по 3 цифры справа налево начиная с младшего разряда.
Затем каждую тройку цифр заменяем соответственно цифрой восьмеричной системы счисления.
Дробную часть разбиваем от запятой вправо на группы по 3 цифры.
Обратный переход - от восьмеричной системы счисления к двоичной - осуществляется заменой каждой восьмеричной цифры ее двоичным эквивалентом (тремя двоичными цифрами).
Для шестнадцатеричной системы счисления - четырьмя двоичными цифрами.
Таблицы переводов
Двоичная - восьмеричная
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Двоичная - шестнадцатеричная
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
Примеры:
1) Переведите двоичные числа в восьмеричную ситему счисления.
a) ![]()
б) ![]()
2) Переведите двоичные числа в шестнадцатеричную систему счисления.
a) ![]()
б) ![]()
Перевод смешанных чисел.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример: Перевести десятичное число 315,1875 в восьмеричную и в шестнадцатеричную системы счисления. Из рассмотренных выше примеров следует: 315.187510=473.148=13B.316 .
Основные арифметические операции:
Рассмотрим основные арифметические операции: сложение, вычитание,умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Таблицы сложения легко составить, используя Правило Счета.
|
Сложение в двоичной системе
|
Сложение в восьмеричной системе
|
|
Сложение в шестнадцатиричной системе
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. |
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
![]()
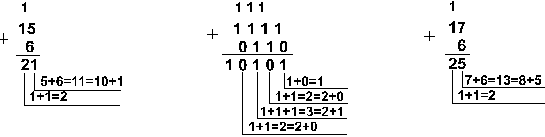
|
Шестнадцатеричная: F16+616
|
Ответ: 15+6 = 2110 = 101012 = 258= 1516. Проверка. Преобразуем полученные суммы к десятичному виду: |
Пример 2. Сложим числа 15, 7 и 3.
![]()
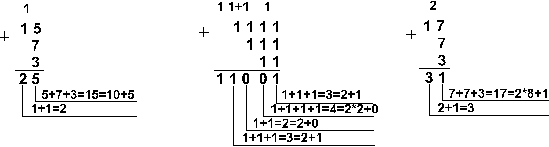
|
Шестнадцатеричная: F16+716+316
|
Ответ: 5+7+3 = 2510 = 110012 = 318= 1916. Проверка: |
Пример 3. Сложим числа 141,5 и 59,75.
![]()

![]()
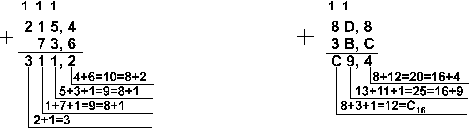
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20
+ 2-2 = 201,25
311,28 = 3*82 + 1•81 + 1*80 + 2*8-1
= 201,25
C9,416 = 12*161 + 9*160 + 4*16-1
= 201,25
Пример 1. Вычтем единицу из чисел 102, 108 и 1016
![]()
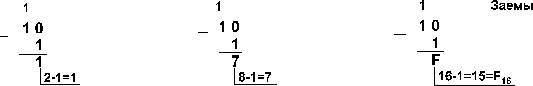
Пример 2. Вычтем единицу из чисел 1002, 1008 и 10016.
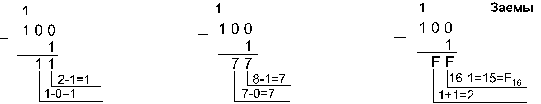
![]()
Пример 3. Вычтем число 59,75 из числа 201,25.
![]()
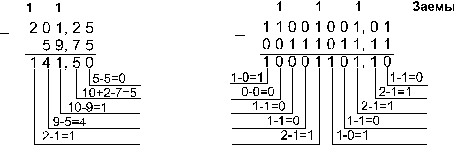
![]()

Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20
+ 2–1 = 141,5;
215,48 = 2*82 + 1*81 + 5*80 + 4*8–1
= 141,5;
8D,816 = 8*161 + D*160 + 8*16–1
= 141,5.
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
|
Умножение в двоичной системе
|
Умножение в восьмеричной системе
|
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример1. Перемножим числа 5 и 6.
![]()
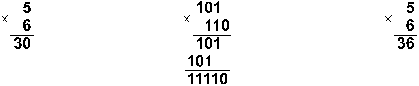
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21
= 30;
368 = 3•81 + 6•80 = 30.
Пример 2. Перемножим числа 115 и 51.
![]()
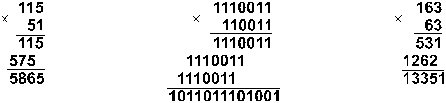
Ответ: 115*51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29
+ 27 + 26 + 25 + 23 + 20
= 5865;
133518 = 1*84 + 3*83 + 3*82 + 5*81
+ 1*80 = 5865.
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 1. Разделим число 30 на число 6.
![]()
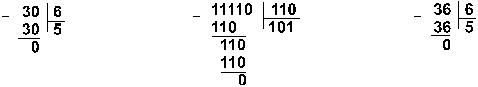
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 2. Разделим число 5865 на число 115.
![]()
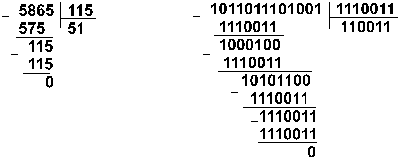
Восьмеричная: 133518 :1638
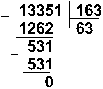
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20
= 51; 638 = 6*81 + 3*80 = 51.
Пример 3. Разделим число 35 на число 14.

![]()
Восьмеричная: 438 : 168
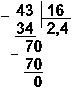
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2*80 + 4*8-1 = 2,5.