Численное дифференцирование.

Решить задачу Коши для дифференциального уравнения y'=f(x, y) на отрезке [a, b] при заданном начальном условии y(a)=c и шаге интегрирования h.
1. Использовать метод Эйлера с шагом h и 2h.
2. Использовать метод Эйлера-Коши с шагом h и 2h.
3. Использовать метод Рунге-Кутта 4 порядка с шагом h и 2h.

Найдите точные значения функции на каждом шаге интегрирования и сформулируйте вывод о зависимости результата от шага и от метода интегрирования.

Варианты работ

1. f(x,y)=xy - x , a=4, b=5, c=0.7, h=0.1
   Точное решение: y = 1 - 0.000100639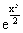
2. f(x,y)=4x2 + 1 - 3y, a=2.6, b=4.6, c=1.8, h=0.2
   Точное решение: y =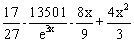
3. f(x,y)= 1.5·x - y - 1.3 , a= - 1, b=1, c=0.2, h=0.2
   Точное решение: y =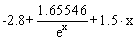
4. f(x,y)=x + y , a=2, b=3, c=1.2, h=0.1
   Точное решение: y=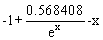
5. f(x,y)=e^-x-1 + 2y , a=0, b=0.5, c=0.3, h=0.05
   Точное решение: y =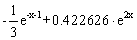
6. f(x,y)=1.5·y + x + 1.4 , a=1, b=2, c=0.9, h=0.1
   Точное решение: y = 0.656994·e^1.5x - 0.666667·(2.06667 + x)
7. f(x,y)=4.1·x - y + 1.6 , a=0.6, b=2.6, c=3.4, h=0.2
   Точное решение: y = - 2.5 + 6.26809·e^-x + 4.1·x
8. f(x,y)= 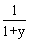, a=1.5, b=2, c=2.1, h=0.05
   Точное решение: y =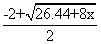
9. f(x,y)= 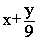, a=2.1, b=3.1, c=2.5, h=0.1
   Точное решение: y =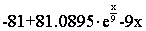
10. f(x,y)= 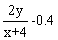, a=3, b=5, c=1.7, h=0.2
    Точное решение: y=1.6+0.4·x-0.022449(4+x)²
11. f(x,y)=2.5·x + y + 0.6, a=1, b=3,c=1.5,h=0.2
    Точное решение:y=-3.1+2.61194·e^x-2.5x
12. f(x,y)=x + 2.5·y + 2, a=1, b=2, c=0.9, h=0.1
    Точное решение: y = 0.185512·e^2.5x - 0.96-0.4·x
13. f(x,y)=2 - x - y , a=2, b=3, c=2.3, h=0.1
    Точное решение: y = 3+9.60577·e^-x-x
14. f(x,y)=y + 1 , a=0.1, b=0.5, c=1.25, h=0.05
    Точное решение: y = - 1 + 2.03588·e^x
15. f(x,y)= 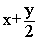, a=-2, b=-1, c=3, h=0.1
    Точное решение: y=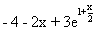
16. f(x,y)=x² + 0.5·y + 1 , a=0, b=2, c=2.9, h=0.2
    Точное решение: y=20.9·e^0.5x - 18 - 8x - 2x²
17. f(x,y)=x + y + 1.5 , a=1.5, b=2.5, c=0.5, h=0.1
    Точное решение: y = - 2.5 + 1.00409·e^x-x

назад содержание вперед