Основные формулы численного
дифференцирования для функции, заданной аналитически[1]
![]() — разность вперед.
— разность вперед.
![]() — разность назад.
— разность назад.
![]() — симметричная разность.
— симметричная разность.
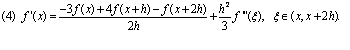
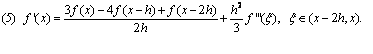
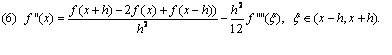
Формулы численного дифференцирования для
равноотстоящих точек,
выраженные через значения функции в этих
точках
Пусть
точки x0, x1, x2, ..., xn - равноотстоящие, т.е. xi+1-xi=h (i=0, 1, 2, .. , n-1), и пусть для функции y=f(x) известны значения yi=f(xi) (i=0, 1, ...,n). Формулы (1)-(6) перепишем в следующем виде:
(1а) ![]()
(2a) ![]()
(3a) ![]()
(4a) ![]()
(5a) ![]()
(6a) ![]()
Задание 6
1.
Вычислить приближенно значения:
а) первой производной функции y=f(x) с порядком погрешности O(h) и O(h2) при i=0,1,...,n.
б) второй
производной функции y=f(x) с порядком
погрешности O(h2) при i=1,...,n-1.
Напечатать таблицу значений узлов, "точных"
значений производных в узлах, приближенных значений производных и их разностей
(фактические погрешности) (см. образец). Проверить результаты на многочленах
соответствующих степеней. Объяснить полученные результаты.
|
Численное
дифференцирование |
|||||||||
|
|
|
|
|
h= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x)=x^2+3 |
|
|
|
|
|
|
|
|
|
x |
f(x) |
f’(x) |
O(h) |
O(h2) |
f''(x) |
fxx O(h2) |
f''(x)-fxx |
||
|
fx |
f’(x)-fx |
fx |
f’(x)-fx |
||||||
|
0 |
3 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
0,1 |
3,1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,2 |
3,2 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,3 |
3,3 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,4 |
3,4 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,5 |
3,5 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,6 |
3,6 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,7 |
3,7 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,8 |
3,8 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0,9 |
3,9 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
4 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
f(x)=x^2+3 |
|
|
|
|
|
|
|
|
|
x |
f(x) |
f’(x) |
O(h) |
O(h2) |
f''(x) |
fxx O(h2) |
f''(x)-fxx |
||
|
fx |
f’(x)-fx |
fx |
f’(x)-fx |
||||||
|
0 |
3 |
0 |
0,1 |
-0,1 |
-4E-15 |
0 |
2 |
|
|
|
0,1 |
3,01 |
0,2 |
0,3 |
-0,1 |
0,2 |
0 |
2 |
2 |
0 |
|
0,2 |
3,04 |
0,4 |
0,5 |
-0,1 |
0,4 |
0 |
2 |
2 |
0 |
|
0,3 |
3,09 |
0,6 |
0,7 |
-0,1 |
0,6 |
0 |
2 |
2 |
0 |
|
0,4 |
3,16 |
0,8 |
0,9 |
-0,1 |
0,8 |
0 |
2 |
2 |
0 |
|
0,5 |
3,25 |
1 |
1,1 |
-0,1 |
1 |
0 |
2 |
2 |
0 |
|
0,6 |
3,36 |
1,2 |
1,3 |
-0,1 |
1,2 |
0 |
2 |
2 |
0 |
|
0,7 |
3,49 |
1,4 |
1,5 |
-0,1 |
1,4 |
0 |
2 |
2 |
0 |
|
0,8 |
3,64 |
1,6 |
1,7 |
-0,1 |
1,6 |
0 |
2 |
2 |
0 |
|
0,9 |
3,81 |
1,8 |
1,9 |
-0,1 |
1,8 |
0 |
2 |
2 |
0 |
|
1 |
4 |
2 |
1,9 |
0,1 |
2 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x)=x^3+3 |
|
|
|
|
|
|
|
|
|
x |
f(x) |
f’(x) |
O(h) |
O(h2) |
f''(x) |
fxx O(h2) |
f''(x)-fxx |
||
|
fx |
f’(x)-fx |
fx |
f’(x)-fx |
||||||
|
0 |
3 |
0 |
0,01 |
-0,01 |
-0,02 |
0,02 |
0 |
|
|
|
0,1 |
3,001 |
0,03 |
0,07 |
-0,04 |
0,04 |
-0,01 |
0,6 |
0,6 |
0 |
|
0,2 |
3,008 |
0,12 |
0,19 |
-0,07 |
0,13 |
-0,01 |
1,2 |
1,2 |
0 |
|
0,3 |
3,027 |
0,27 |
0,37 |
-0,1 |
0,28 |
-0,01 |
1,8 |
1,8 |
0 |
|
0,4 |
3,064 |
0,48 |
0,61 |
-0,13 |
0,49 |
-0,01 |
2,4 |
2,4 |
0 |
|
0,5 |
3,125 |
0,75 |
0,91 |
-0,16 |
0,76 |
-0,01 |
3 |
3 |
0 |
|
0,6 |
3,216 |
1,08 |
1,27 |
-0,19 |
1,09 |
-0,01 |
3,6 |
3,6 |
0 |
|
0,7 |
3,343 |
1,47 |
1,69 |
-0,22 |
1,48 |
-0,01 |
4,2 |
4,2 |
0 |
|
0,8 |
3,512 |
1,92 |
2,17 |
-0,25 |
1,93 |
-0,01 |
4,8 |
4,8 |
0 |
|
0,9 |
3,729 |
2,43 |
2,71 |
-0,28 |
2,44 |
-0,01 |
5,4 |
5,4 |
0 |
|
1 |
4 |
3 |
2,71 |
0,29 |
2,98 |
0,02 |
6 |
|
|
2. Пользуясь одной из формул (1)-(6) в
заданной точке х вычислить разностную производную первого или второго порядка,
последовательно уменьшая шаг h (например, вдвое) до тех пор, пока фактическая
погрешность не начнет возрастать. Определить h оптимальное экпериментально и теоретически, объяснить
полученные результаты.
Пример
При использовании формулы (4) в результате ошибки e, допускаемой в каждом из значений функции, оценка для
суммарной погрешности будет выглядеть следующим образом:
![]()
Оптимальный шаг, т.е. такой, при котором
обеспечивается минимальная суммарная погрешность, находится обычным образом,
как решение задачи на экстремум.
Напечатать
"точное" значение производной точке х,
таблицу значений h, уменьшая h, например, вдвое,
приближенных значений
производной в точке х,
их разностей (фактические
погрешности) (см. образец).
|
Выбор шага (формула 4) |
x= |
1 |
h0= |
|
|||
|
f(x)=exp(2*x) |
f'(1)= |
14,778112 |
|
h_opt |
|
|
|
|
h |
0,1 |
0,05 |
0,025 |
0,0125 |
0,00625 |
0,003125 |
0,001563 |
|
fx O(h2) |
14,5484 |
14,7249 |
14,765 |
14,774 |
14,7768 |
14,7744 |
14,7712 |
|
погр. |
0,22971 |
0,05321 |
0,0131122 |
0,0037 |
0,0013122 |
0,003712 |
0,006912 |
|
|
|
|
|
|
|
|
|
|
eps= |
5E-06 |
|
M3= |
|
hopt= |
0,006981 |
|
3. Дифференцированием
интерполяционного многочлена в форме Ньютона получить формулу численного
дифференцирования для вычисления приближенного
значения производной заданного
порядка с заданным порядком аппроксимации в заданной точке. Проверить формулу
на многочленах соответствующих степеней.
а) с=х0; b)с=х1;
c) с=x2; d) с=(x1+x2)/2; e) с=xn, f) с=хn-1; g) с=(xn+xn-1)/2).